Определение оптимальной траектории

Теперь мы будем выявлять самое главное - оптимальную траекторию. Нам нужно проехать дистанцию за минимальное время.

Сперва, рассмотрим движение на повороте, т.е. движение по окружности. В связанной с лыжником системе отсчета, введем центробежную силу (F цб), направленную от центра дуги, равную:

*U/R,

где – R радиус дуги.

Центр тяжести лыжника в этой системе неподвижен: значит, в любой момент времени равнодействующая приложенных сил равно нулю. Поэтому сила реакции снега должна быть направлена к центру дуги - ведь это единственная сила, которая может скомпенсировать Fцб. У саночников это обеспечивается наклоном желоба. А у лыж для лучшего сцепления со снегом скользящая поверхность имеет металлические канты.

Лыжник на повороте испытывает большую нагрузку. Суммарная перегрузка превышает 2g, то есть примерно равна удвоенному весу лыжника. Причем падает она в основном на «внешнею» ногу (попытка встать на внутреннюю лыжу, обычно заканчивается падением). Почему лыжника, скатывающегося с горы, нельзя уподобить, скажем, бусинке, соскальзывающей по гладкой изогнутой проволоке? В первую очередь, потому, что он сам выбирает маршрут движения в коридоре, заданном флагами (у саночников - желобом). Спортсмену (даже если считать его материальной точкой) предстоит найти оптимальную траекторию, в то время как движение бусинки чисто одномерное. Вид оптимальной траектории определяется сочетанием целого ряда факторов. Прежде всего, желательно пройти трассу кратчайшим путем, как можно меньше уклоняясь от линии склона (рис.2). При этом мы выигрываем не только из-за сокращения расстояния, но и за счет увеличения средней крутизны маршрута – чем круче склон, тем больше скатывающая сила и тем меньше сила трения. В то время как идеальная линия уже обозначена флажками, слаломисты стараются идти как можно ближе к флагам, отбивая их плечом и корпусом.

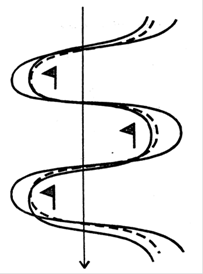
Рис.2. Варианты выбора маршрута на трассе слалома. Пунктиром выделенная кривая – оптимальная траектория.

Можно оценить потерю времени вследствие удлинения пути. Пусть отклонение от оптимальной кривой составляет всего лишь ± 10 см. Того же порядка будет удлинение каждой из образующих ее дуг. На слаломной трассе из 50 ворот при средней скорости 10м/с проигрыш окажется вполне ощутимым, по формуле для нахождения времени посчитаем:

К каждому повороту прибавиться мо 10 см., поворотов 50.

S=50 ×0,1м; U=10 м/с.

t= 0,5 сек.

Проигрыш оказывается ощутимым.

Также нельзя спрямлять участки пути, между флагами. Во- первых, при этом придется сбрасывать скорость, чтоб вписаться в крутой поворот, во-вторых, путь по прямой не всегда быстрее. Ведь тело начинает движение с более крутого участка пути, и получив большое ускорении начинает движение. Путь по дуге длиннее, он начинается с более крутого участка. Бусинка получает большее ускорение, и выигрыш в скорости оказывается важнее, чем проигрыш в расстояние. С этой точки зрения траектория, составленная из плавно сопряженных дуг, также оказывается лучше, чем та, где прямые участки с резкие поворотами.